Sudoku Squares are elegant, and frankly, magical.¹

With pockets of time being freed up with work from home orders during the COVID-19 pandemic, I picked up Sudoku to fill in the gaps. And man, it’s fun solving them - it’s cathartic seeing the numbers fall nicely into place.

It’s one thing to solve Sudokus, but another to create one.

Out of curiosity, I decided to try and make a fully filled Sudoku Grid by hand. I gave up after a few attempts. It’s surprisingly tedious and difficult to build one off the cuff.

Wouldn’t it be much much easier for a computer to do all the tedious comparisons and checks rather than relying on my error-prone brain?

Since I was quite free waiting to enroll into University… one thing led to another, which led to this homemade Sudoku game being born. This is how I made it.

A Lazy Approach

The first approach that came to my mind was basically building the board similar to how I would try doing it by hand. The algorithm’s script is in the repo under sudogen.py.

The Algorithm ⚙️

1. Fill up the grid row by row randomly with valid (unused) numbers that comply with Sudoku rules

2. If the row can’t be built, try making the row again from scratch

3. If the row cannot be built multiple times, give up on the current row and build the previous row from scratch again

4. Repeat until all 9 rows of the Sudoku grid fall into place

This is, admittedly, a very lazy way of building the Sudoku board. It does not keep track of the values that were picked and failed (which means that there is a chance that the row can choose a failed number again). It even ‘gives up’ prematurely, even though a solution to building a row can be found.

But before we work on making the approach more rigorous, let’s make the code work first.

Making the Grid

First things first, we need to set up a empty sudoku grid so that we can fill it in.

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

def generateSudoku():
    # A more elegant way of building the grid
    grid = [[0 for i in range(9)] for j in range(9)]
    # But let's make the grid more human-readable...
    # ...for ease of visualisation/debugging
    grid = [
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0]
    ]
    return grid
# In the source code, the latter approach was used

The next thing we need to do is to build the row. To fill in the cells in the row, we need to find out what the possible (unused) values can be placed in each cell.

Searching the Rows, Columns and Squares

To find the unused numbers that can be inserted, we must search and find out which numbers have appeared in the position’s row, column and square. This is essentially how one would check if their Sudoku answer is correct.

An intuitive approach is to search the row/column/square and check which values already exist, which will implicitly give us the unused values.

This is one way we can implement this if we just checked the row:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

# For a given position (rowIdx, colIdx) on the grid...
def getAvailValues(rowIndex, colIndex, grid):
    unused = [n for n in range(1,10)]
    # Find occurences in a row
    for value in range(1,10):
        # colIndex rather than 2/5/8 for 'early stopping'
        for colPosition in range(colIndex+1):
            if grid[rowindex][colPosition] == value:
                unused.pop(value)
                break
    return unused

This approach is slow. Its worst case time complexity is O(n^2).

This slowness adds up over time when building the Sudoku. This function is the workhorse of the algorithm, as it is called for every position of the Sudoku grid, which means that at least 81 calls need to be made!

So what I did was implement a counting sort.

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def getAvailValues(rowIndex, colIndex, grid):
    vmap = [0 for x in range(10)]
    # Logs occurences in row
    for i in range(colIndex+1):
        vmap[grid[rowIndex][i]] +=1
    unused = []
    for i in range(1,10):
        if vmap[i] == 0:
            unused.append(i)
    return unused

# NOTE: It is entirely possible to range(9) instead.
# range(1,10) was used for clarity's sake 

This allows us to map the values that have been used when scanning through the row, col & squares of the grid. We can then check for a value’s occurence with a O(1) list access to vmap. For example, to find how many times ‘1’ has appeared, I simply need to call vmap[1].

This reduces our time complexity to O(n)².

We can implement this trivially for rows and columns, since we can access a row/column using rowIndex/colIndex. But finding the 3x3 squares is a little harder. First, we need to know where the square starts and stops for the position being queried.

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

# Returns the row/col limits for the cell's square
def getSquareLimits(rowIndex, colIndex):
    rowLimits, colLimits = [],[]
    # Column Limits
    if colIndex < 3:
        colLimits = [0,3]
    elif colIndex < 6:
        colLimits = [3,6]
    else:
        colLimits = [6,9]
    # Row Limits
    # rowIndex is used for early stopping
    if rowIndex < 3:
        rowLimits = [0,rowIndex+1]
    elif rowIndex < 6:
        rowLimits = [3,rowIndex+1]
    else:
        rowLimits = [6,rowIndex+1]
    return (rowLimits, colLimits)

With these limits, we can then implement our counting sort for a 3x3 square in the Sudoku:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

# Get the unused values for the square only
def getAvailValues(rowIndex, colIndex, grid):
    # Get the square limits
    sqLim = getSquareLimits(rowIndex, colIndex)
    for ri in range(sqLim[0][0], sqLim[0][1]):
        for ci in range(sqLim[1][0], sqLim[1][1]):
            vmap[grid[ri][ci]] +=1
    for i in range(1,10):
        if vmap[i] == 0:
            unused.append(i)
    return unused

We can then finally build our overall function that checks for row, column and square:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Main logic for sifting through usable values
def getAvailValues(rowIndex, colIndex, grid):
    # Mapping of number of values that appear
    vmap = [0 for x in range(10)] 

    # Logs occurences in row
    for i in range(colIndex+1):
        vmap[grid[rowIndex][i]] +=1

    # Log occurences in col
    for i in range(rowIndex+1):
        vmap[grid[i][colIndex]] +=1

    # Log occurences in the cell's square
    sqLim = getSquareLimits(rowIndex, colIndex)
    for ri in range(sqLim[0][0], sqLim[0][1]):
        for ci in range(sqLim[1][0], sqLim[1][1]):
            vmap[grid[ri][ci]] +=1

    # Check which values did not appear             
    unused = []
    for i in range(1,10):
        if vmap[i] == 0:
            unused.append(i)
    return unused

Building Row by Row

Let’s start building the grid row by row. From columns 1 to 9, we randomly choose one of the unused values to insert into the grid.

In the likely event that there is no solution where getAvailValues returns an empty list, we execute step 2 of the algorithm: Discard the row and start it again through a recursive call. There is a possibility that the arrangement of previous rows make it such that no permutation of numbers can give a valid Sudoku row. The function will then loop forever in recursion purgatory.

To prevent this, we can keep track of the number of recursions the function has gone through and break it if it passes a certain threshold.³

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

# Generate the sudoku board row in accordance with sdku rules
def generateRow(rowIndex, sudokuGrid):
    global __recursionCounter
    # Break recursion to backtrack and rebuild the previous row
    # Arbitrary number chosen 
    if(__recursionCounter>9):
        return
    for i in range(9):
        pool = getAvailValues(rowIndex, i, sudokuGrid)
        # Recursion managed by the global counter field
        if len(pool)==0:
            # No solution. Re-build row
            __recursionCounter +=1
            sudokuGrid[rowIndex] = [0 for x in range(9)]
            generateRow(rowIndex, sudokuGrid)
        else:
            rdi = randint(0,8)
            if rdi >= len(pool):
                rdi = rdi%len(pool)
            sudokuGrid[rowIndex][i] = pool[rdi]

We can then wrap it up with additional logic to control row generation:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def generateSudoku():
    grid = [
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0],
    [0,0,0,0,0,0,0,0,0]
    ]
    i = 0
    while i<9:
        global __recursionCounter
        if __recursionCounter > 9:
            # Reset the counter
            __recursionCounter = 0
            i-=1
            generateRow(i,grid)
        else:
            generateRow(i,grid)
            i+=1
    return grid

A purely recursive approach (getting generateRow to call itself to build the next row) was dropped in favor of a iterative approach for ease of debugging. Python also tended to just stop going into deeper levels of recursion even when setting the system variable for recursion depth limit to the max.

Running the code with a simple script to print every row, the grid generator works!⁴

At this point, I was ready to wrap up. Mission accomplished, after all. But then a friend of mine who knew I was working on this project showed me this Sudoku backtracking solver.

A Simple Backtrack

I ran the code in the link. It looked very, very impressive, with all the numbers flickering about as the algorithm methodically worked its way to solve the puzzle.

Although my script builds the full board rather than a puzzle with blanks to be solved, perhaps there is a way to implement a backtracking algorithm in the code myself?

The Algorithm ⚙️

A backtracking algorithm essentially tries all possible permutations of a solution and discards the failed attempts. It is typically done through recursion.

1. Build row by row from the leftmost to rightmost cells with randomly chosen values from the set of unused, valid values

2. If a value cannot be found, go back a cell. Blacklist the cell’s previously selected value and proceed with another valid one

3. If no valid value exists for the returned cell after a backtrack, go back another cell. If the cell is the first of the row, go back to the previous row instead and rebuild it from scratch randomly

4. Repeat until the grid is formed

I implemented the ‘backtrack’ non-recursively, using a simple blacklist for a single row:

0

 __blacklistedVals = [[0 for x in range(10)] for x in range(9)]

For every column index, failed values get logged into the blacklist and are excluded when getAvailValues() is being called in the event of a backtrack:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def getAvailValues(rowIndex, colIndex, grid):
    global __blacklistedVals
    vmap = [0 for x in range(10)] #0-9 so 10 vals
    sqLim = getSquareLimits(rowIndex, colIndex)
    # Logs occurences in row
    for i in range(0,colIndex+1):
        vmap[grid[rowIndex][i]] +=1
    # Log occurences in col
    for i in range(0,rowIndex+1):
        vmap[grid[i][colIndex]] +=1
    # Log occurences in the cell's square
    for ri in range(sqLim[0][0], sqLim[0][1]):
        for ci in range(sqLim[1][0], sqLim[1][1]):
            vmap[grid[ri][ci]] +=1
    unused = []
    for i in range(1,10):
        if vmap[i] == 0 and __blacklistedVals[colIndex][i]==0:
            unused.append(i)
    return unused

The row generating logic dropped the recursion in favor of an iterative approach which is somewhat easier to debug:

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

def generateRow(rowIndex, grid):
    global __blacklistedVals
    i = 0
    # Cell controller
    while i<9:
        pool = getAvailValues(rowIndex, i, grid)
        if(len(pool)==0):
            # No solution.
            # Backtrack one cell, blacklist the prev value and try again
            __blacklistedVals[i] = [0 for x in range(10)]
            i-=1
            if i<0:
                return True

            __blacklistedVals[i][grid[rowIndex][i]] +=1
            grid[rowIndex][i] = 0

        else:
            rdi = randint(0,8)
            if rdi >= len(pool):
                rdi = rdi%len(pool)
            grid[rowIndex][i] = pool[rdi]
            i+=1

    return False

# The bool returns are used to control the overall grid generation logic
def generateSudoku():
    # grid = [...] is omitted
    i = 0
    while i < 9:
        if generateRow(i, grid):
            # Row has failed to build. Re-build the previous row and blacklist
            grid[i] = [0 for x in range(9)]
            __blacklistedVals = [[0 for x in range(10)] for x in range(9)]
            i-=1
            grid[i] = [0 for x in range(9)]
        else:
            i+=1
    return grid

Running the script, it works! But what if we were more rigorous with the depth of the blacklist?

Mother Of All Backtracks (MOAB)

Instead of keeping track of a row’s worth of failed solutions, how about we extend it to the whole grid?

0

 __blacklistedVals = [[[0 for x in range(10)]for y in range(9)]for z in range(9)]

This particular implementation was pretty hairy, with the backtracking logic extending out to 2 seperate functions. In the repo, this is sudogen3 if you are interested in the full implementation code.

The Algorithm ⚙️

1. Build row by row from the leftmost to rightmost cells with randomly chosen values from the set of unused, valid values

2. If a value cannot be found, go back a cell. Blacklist the cell’s previously selected value and proceed with another valid one

3. If no valid value exists for the returned cell after a backtrack, go back until we reach a cell with valid values

4. Repeat until the grid is formed

This was a can of worms. Additional flags and conditions needed to be added to catch perculiar edge cases, such as infinite loops⁵ that the algorithm could get stuck in.

 0
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

# A quick showcase of the additional functions

def backtrackRow(rowIndex):
    global __blacklistedVals
    # Reset row blacklist
    __blacklistedVals[rowIndex] = [[0 for x in range(10)] for y in range(9)]
    return rowIndex-1

# Backtrack cell by cell until we have a pool of > 1 possible value
# Rare edge case whereby the backtrack cycles about a cell. The rows are built with no solution.
# This + other possible undefined edge cases are caught by the infiniteLoop flag.
def backtrackCell(rowIndex, colIndex, grid, infiniteLoop):
    if(colIndex<0):
        # Backtrack a row as current row has no solution
        rowIndex = backtrackRow(rowIndex)
        colIndex = 8
    pool = getAvailValues(rowIndex, colIndex, grid)
    if len(pool) > 1 and not infiniteLoop:
        return [rowIndex, colIndex]
    else:
        infiniteLoop = False
        grid[rowIndex][colIndex] = 0
        return backtrackCell(rowIndex, colIndex-1, grid, infiniteLoop)

def generateSudoku():
    # grid = [...] is omitted
    global __blacklistedVals
    global __infiniteRecursion
    i = 0
    specificIndex = 0
    new_coords = []
    while i<9:
        if generateRow(i, grid, specificIndex):
            i = backtrackRow(i)
            if i<0:
                for x in range(9):
                    print (grid[x])
                break
            tmp = backtrackCell(i, 8, grid, __infiniteRecursion)
            # Oscillation infinite loop catcher
            if new_coords == tmp:
                __infiniteRecursion = True
            else:
                __infiniteRecursion = False
                new_coords = tmp
                specificIndex = new_coords[1]
                i = new_coords[0]
        else:
            specificIndex = 0
            i+=1
    __blacklistedVals = make_new_blacklist()
    return grid

Visualising Efficiency

The fun part comes when we take a look at the data we can get from the algorithms.

To check the efficiency of the 3 different generators, I created a counter variable __timesCalled that records the amount of times getAvailValues() is being called. This is because getAvailValues() is indicative of the algorithm’s efficiency since it is called for every single cell input.

All the effort into making a thorough, methodical Sudoku generator must pay off in terms of efficiency, right?

After all, it intuitively makes sense that with a proper backtracking algorithm, we can systematically search through values and quickly converge to a valid sudoku square. It should at least be better than randomly re-building rows, leaving it up to chance.

Well, no.

It was kind of obvious while debugging the three algorithms that the MOAB and Simple Blacklist algorithms were slow.

For each of the 3 Sudoku algorithms discussed, 1000 puzzles were generated and the number of lookup calls to getAvailValues() were recorded down.

Here’s the scatter plot of the Lazy Approach, Simple Backtrack and MOAB.

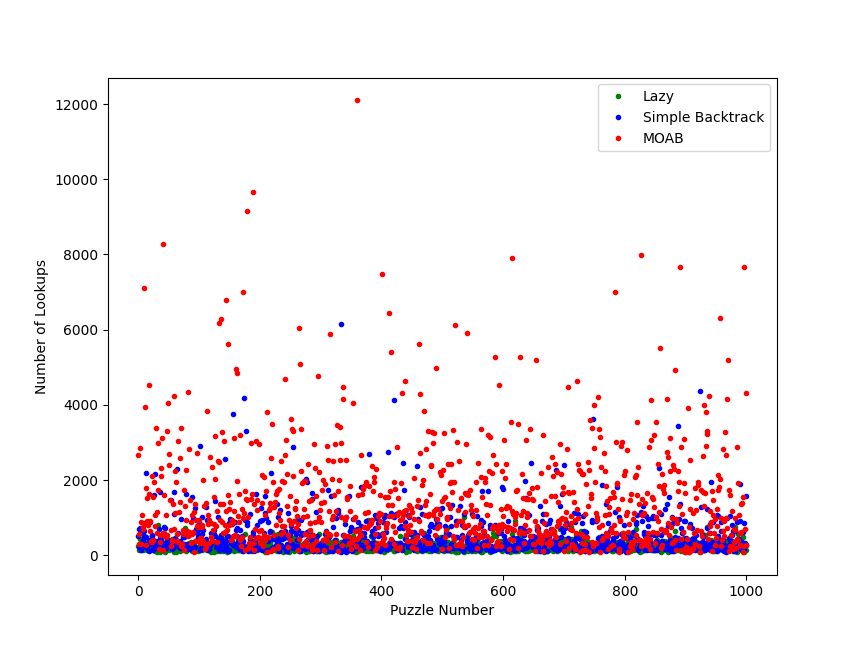
There’s a lot of noise, but it is abundantly clear that the blacklisting approaches are generally less efficient than the Lazy Approach.

Let’s plot a Box & Whisker diagram to get a cleaner look into the stats.

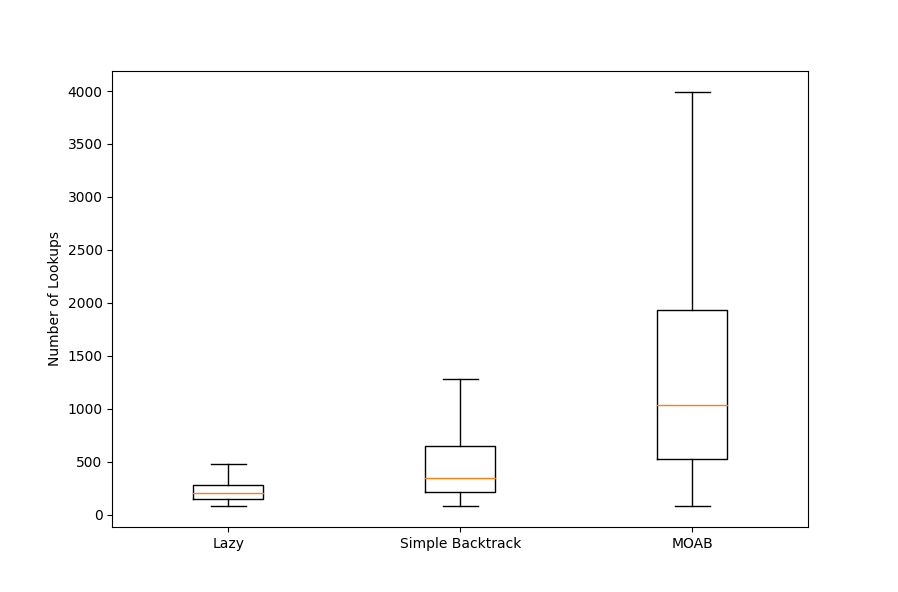
With this, it is clear that on average, the Lazy Approach takes much fewer lookups than the Simple Blacklist and MOAB. But why?

Perhaps its because it’s more likely for the algo to stumble onto the ‘correct’ sequence of values randomly for any given row rather than be going through all the possible permutations using the backtracking algo. Especially at the later rows where there may only be one ‘valid’ sequence of values that exists and will naturally converge to a solution, but many wrong values to choose from and permutate through.

On Efficiency

To begin with, backtracking is a naiive approach to solving problems, at least in the case of Sudoku. Backtracking is a form of brute forcing, which is inefficient from the get-go.

There are opportunities for more elegant ways to build the grid using the properties of Sudoku, such as reflections, rotations & group-theory. There are a wide range of papers and studies for Sudoku that go into detail on finding all sorts of permutations for valid Sudoku grids which can further advise Sudoku generating algorithms. The perfect build case for my scripts are 81 lookup calls, but it is entirely possible to go below 81 lookups and reach really high levels of efficiency.

Of course, I’m pretty sure that out there in the wild, people have already created Sudoku generating algorithms that exploit its mathematical properties to dizzying levels of efficiency.

Puzzle-Making and Tkinter

At this point I’ve spent a considerable amount of time building and debugging this program. Why not just make it into a proper game? To wrap this project up, I made the UI using Tkinter and made it into a fully functional game with varying difficulty.

The puzzle is formed by calling the sudoku grid generator, then popping off random positions from the grid. The higher the difficulty, the more positions popped.

This is a naiive approach to accessing difficulty. A true reflection of difficulty not only scales with the number of blanks, but also takes into account the techniques that a player needs to use to solve the puzzles. But for my intents and purposes, the naiive approach should still get the job done for a vast majority of the time.

If you’re interested to try my homemade Sudoku out, download my project here and enjoy! 🍻